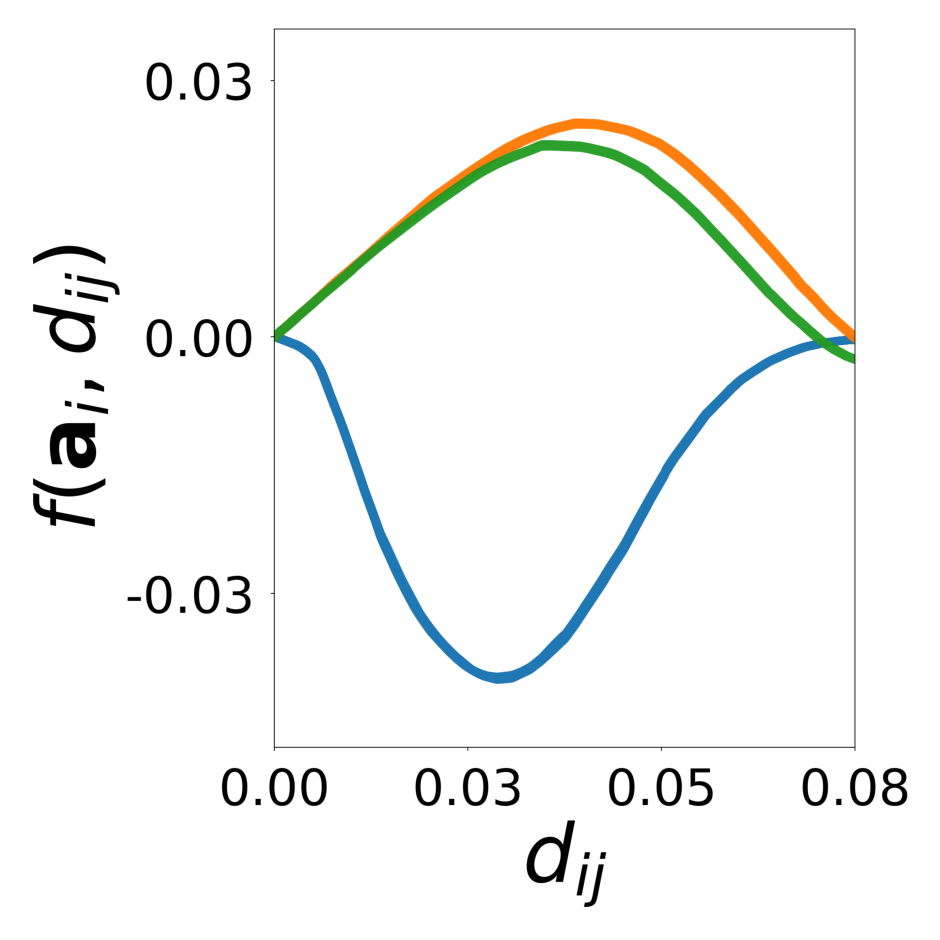
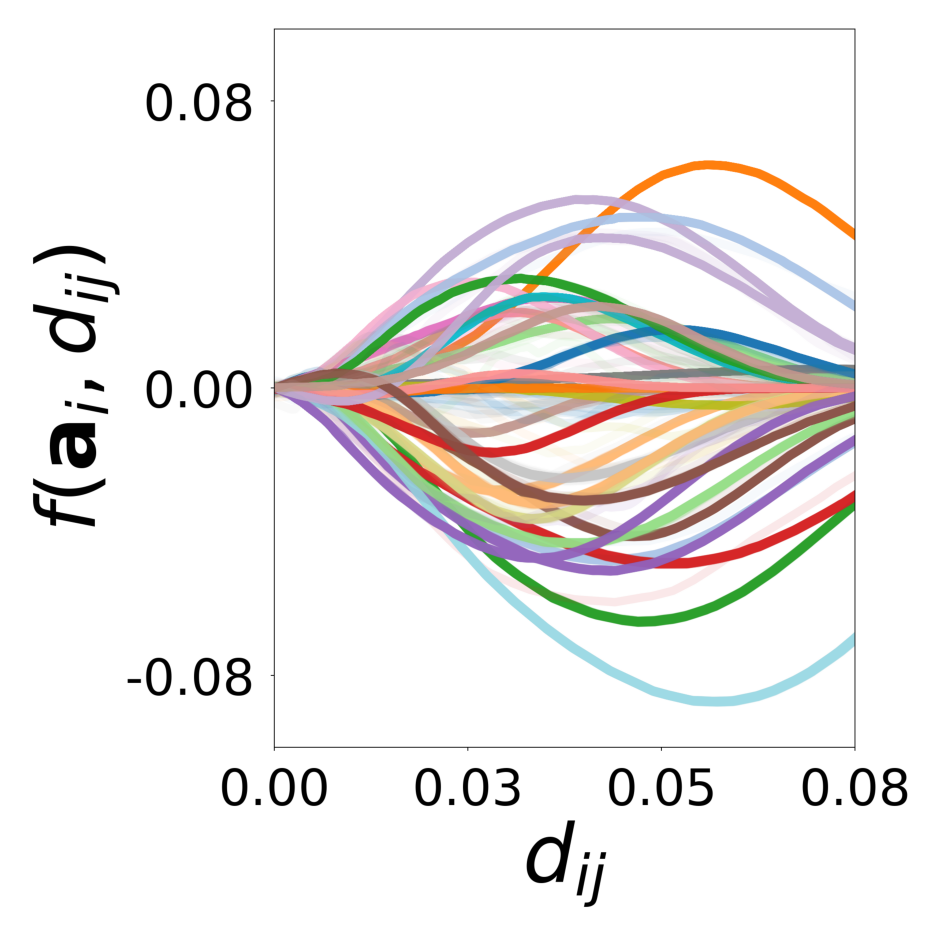
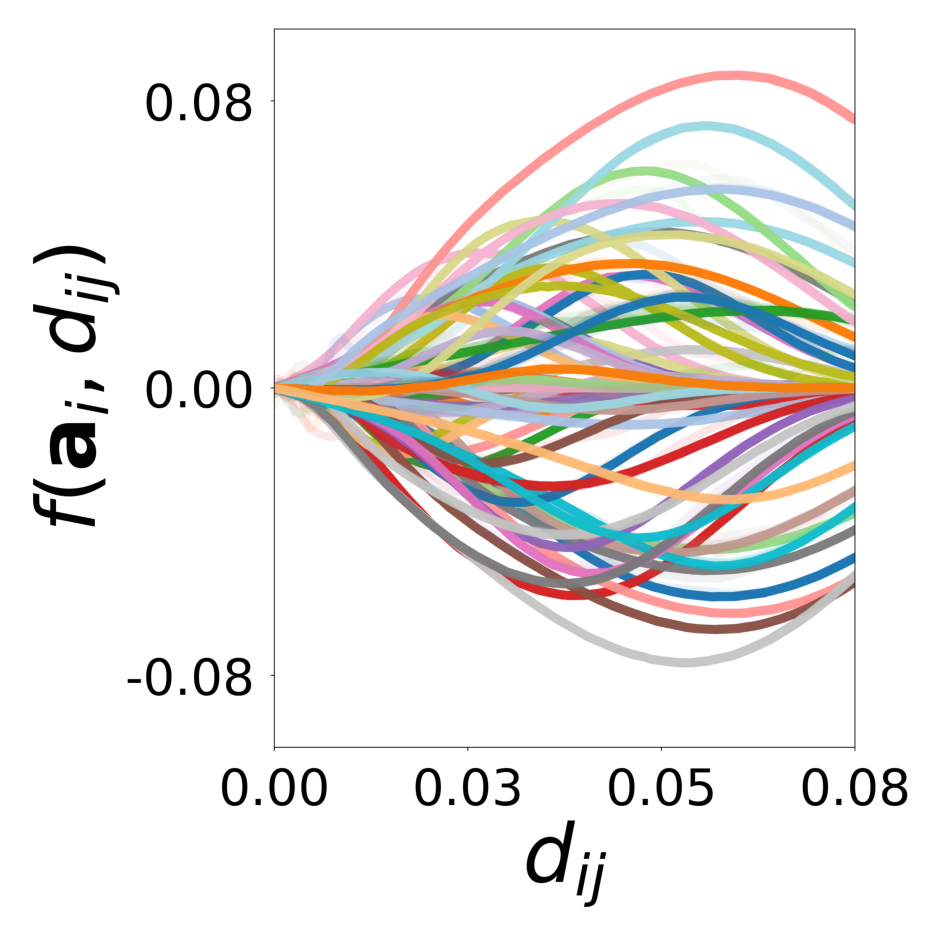
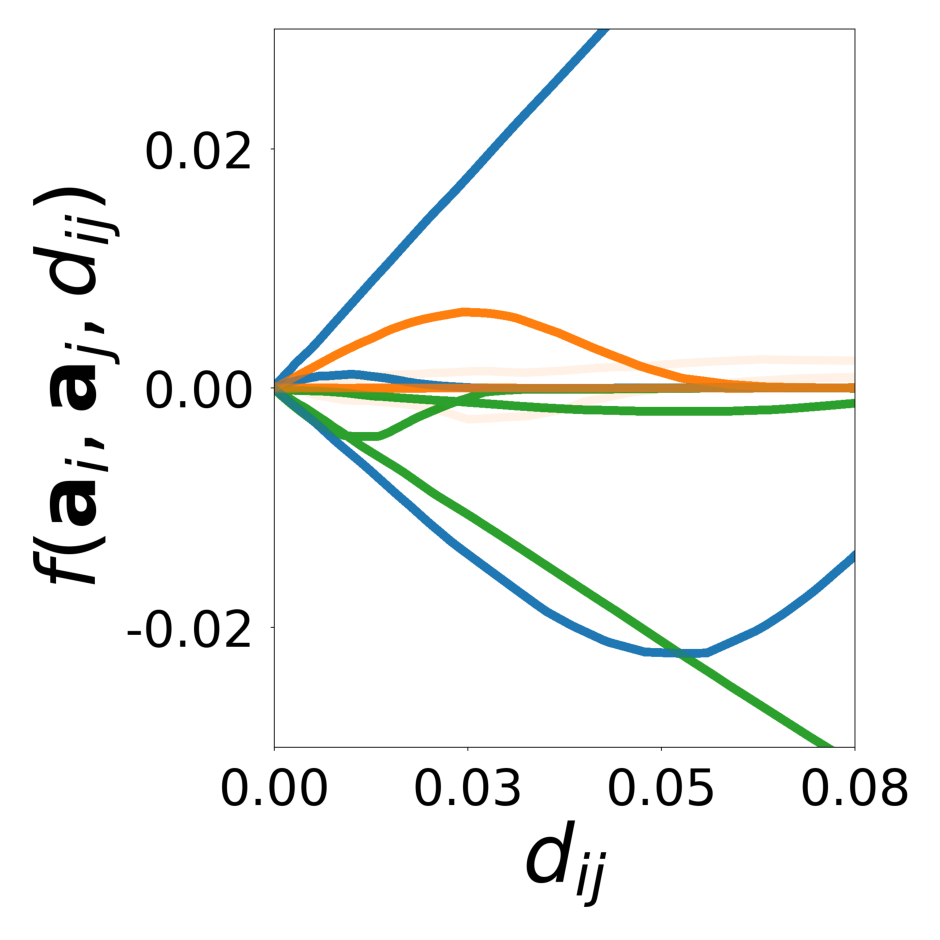
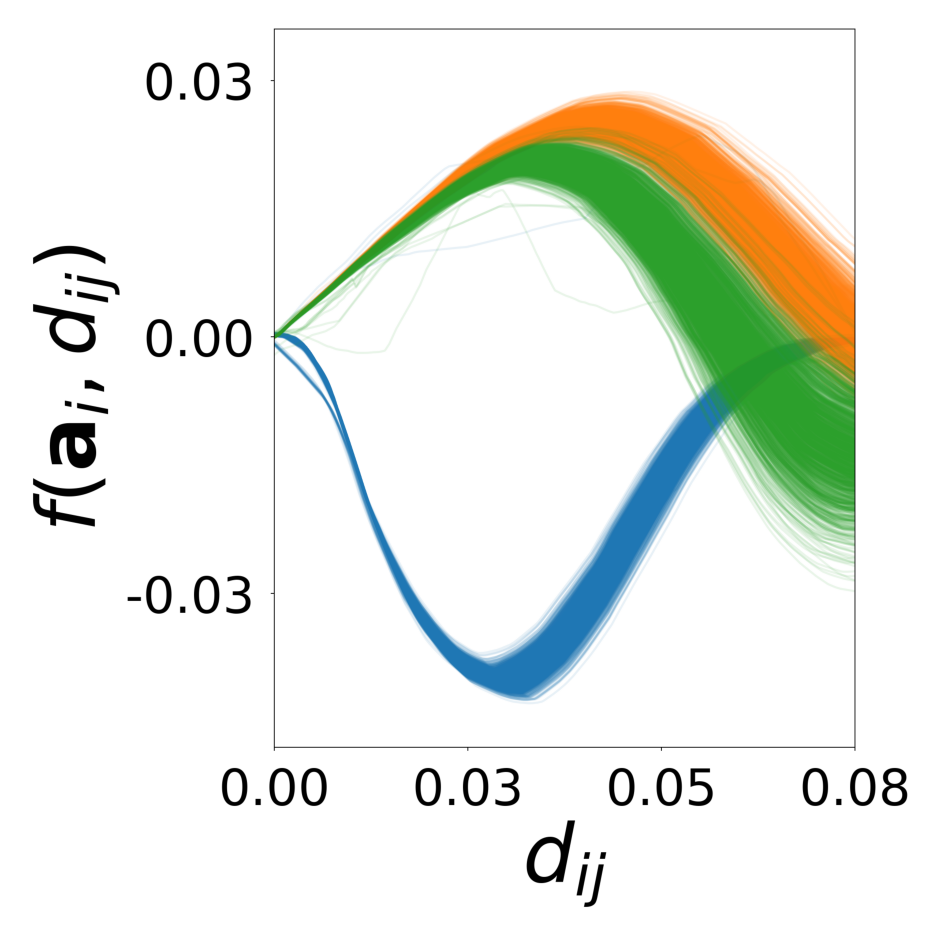
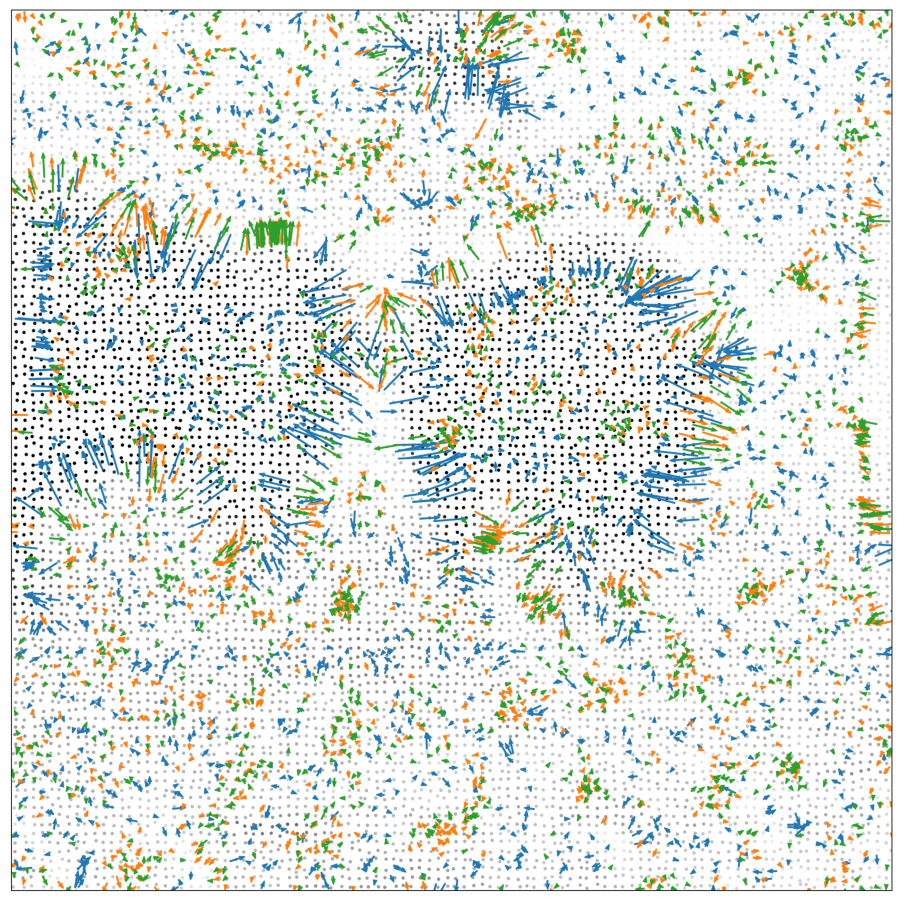
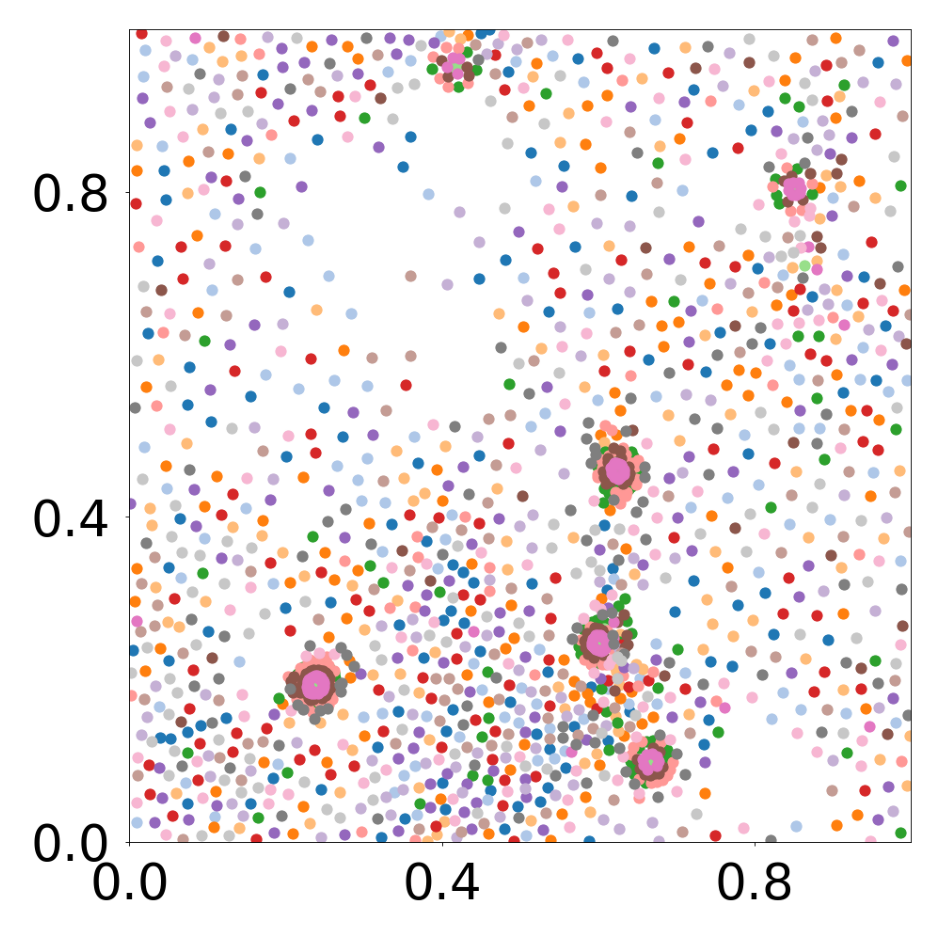
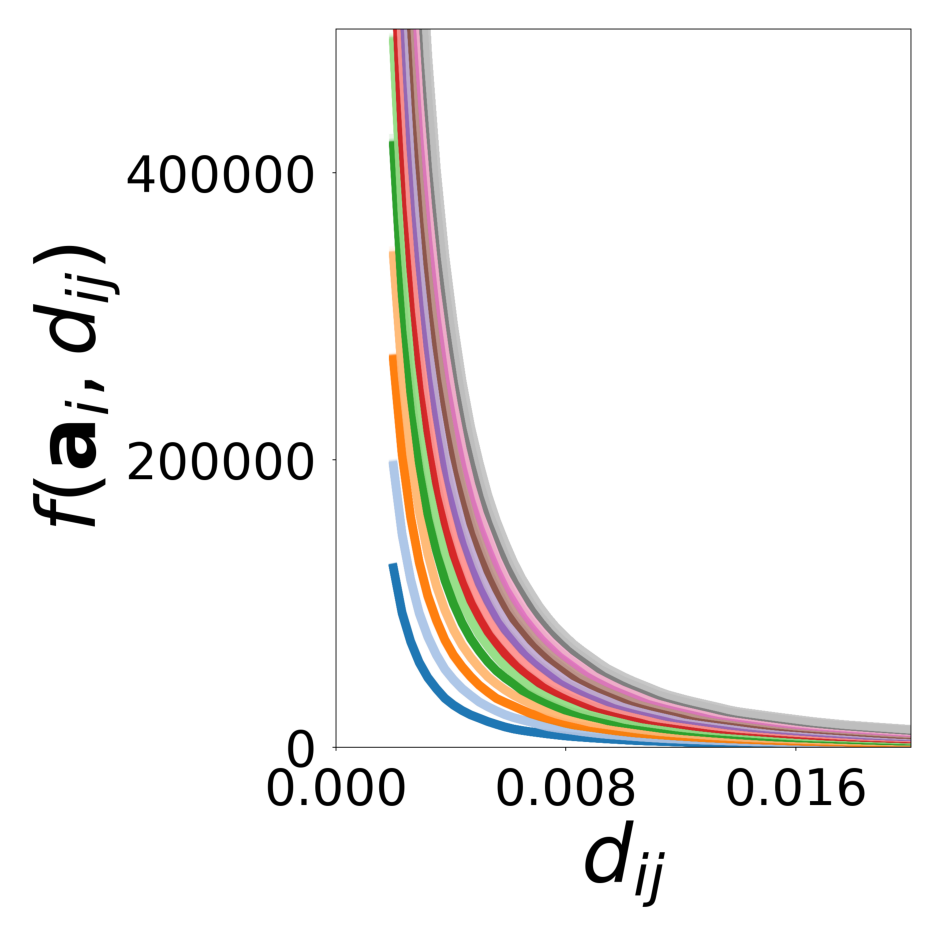
Decomposing heterogeneous dynamical systems with graph neural networks

This site shows the code to generate some figures from the “Decomposing heterogeneous dynamical systems with graph neural networks” paper.

We showed with a diverse set of simulations that message passing GNNs that jointly learn interaction, update functions and latent node properties are a flexible tool to predict, decompose, and eventually understand complex dynamical systems. With the currently available PyTorch Geometric software libraries, it is straightforward to implement a differentiable architecture and loss that encode useful assumptions about the structure of the complex system such as local connectivity rules or the location of learnable and known functions and their inputs. In particular, a well designed GNN can learn a low-dimensional embedding of complex latent properties required to parameterize heterogeneous particle-particle interactions. The learned embeddings can be used to reveal the structure of latent properties underlying the complex dynamics and to infer the corresponding parameters. It is possible to dissect the dynamical system and conduct virtual experiments with arbitrary compositions of particles and interactions. This ability will be particularly important for understanding the behavior of heterogeneous dynamical systems in biology that can only be observed in their natural, mixed configurations. Examples include bacterial community organization, embryonic development, neural networks, and the social interactions of animal communities, which cannot be studied in isolation.

Attraction-repulsion system with 3 particle types

Particles

Simulation

This script creates the first column of paper’s Figure 2. Simulation of an attraction-repulsion system, 4800 particles, 3 particle types.

create_fig_2_1.py

Boids system with 16 different particle types

Particles

Simulation

This script creates the fourth column of paper’s Figure 2. Simulation of boids (https://en.wikipedia.org/wiki/Boids), 1792 particles, 16 types.

create_fig_2_4.py

Coulomb-like system with different particle charges

Particles

Simulation

This script creates the third column of paper’s Figure 2. Simulation of a Coulomb-like system: 960 particles, 3 different charges.

create_fig_2_3.py

Generalization test of GNN trained on boids

Particles

Generalization Test

This script generates figures shown in Supplementary Figures 13. This is a generalization test of the GNN trained with the boids simulation . As a generalization test, the…

create_fig_boids_supp13.py

Gravity-like system with different particle masses

Particles

Simulation

This script creates the second column of paper’s Figure 2. Simulation of a gravity-like system, 960 particles, 16 different masses.

create_fig_2_2.py

Reaction-diffusion propagation with different diffusion coefficients

Mesh

Simulation

This script creates the sixth column of paper’s Figure 2. Simulation of reaction-diffusion over a mesh of 1E4 nodes with variable propagation-coefficients.

create_fig_2_6.py

Signaling system with 998 nodes

Signaling

Simulation

This script creates the seventh column of paper’s Figure 2. Simulation of a signaling network, 986 nodes, 17,865 edges, 2 types of nodes. Note 100 of datasets are generated…

create_fig_2_7.py

Training GNN on Coulomb-like system

Particles

GNN Training

This script generates figures shown in Supplementary Figure 8. A GNN learns the motion rules governing a gravity-like system The simulation used to train the GNN consists of…

create_fig_coulomb.py

Training GNN on attraction-repulsion (16 particle types)

Particles

GNN Training

This script creates the fourth column of Figure 3. A GNN learns the motion rules of an attraction-repulsion system. The simulation used to train the GNN consists of 4800…

create_fig_3_4.py

Training GNN on attraction-repulsion (3 particle types)

Particles

GNN Training

This script creates the first column of paper’s Figure 3. A GNN learns the motion rules of an attraction-repulsion system. The simulation used to train the GNN consists of…

create_fig_3_1.py

Training GNN on attraction-repulsion (32 particle types)

Particles

GNN Training

This script creates the fifth column of paper’s Figure 3. A GNN learns the motion rules of an attraction-repulsion system. The simulation used to train the GNN consists of…

create_fig_3_5.py

Training GNN on attraction-repulsion (64 particle types)

Particles

GNN Training

This script creates the sixth column of paper’s Figure 3. A GNN learns the motion rules of an attraction-repulsion system. The simulation used to train the GNN consists of…

create_fig_3_6.py

Training GNN on attraction-repulsion (asymmetric, 3 particle types)

Particles

GNN Training

This script creates the second column of paper’s Figure 3. A GNN learns the motion rules of an asymmetric attraction-repulsion system The simulation used to train the GNN…

create_fig_3_2.py

Training GNN on attraction-repulsion (continuous function domain)

Particles

GNN Training

This script creates the third column of paper’s Figure 3. A GNN learns the motion rules of an attraction-repulsion system. The simulation used to train the GNN consists of…

create_fig_3_3.py

Training GNN on attraction-repulsion (hidden field)

Particles

GNN Training

This script creates figure of paper’s Figure 4. A GNN learns the motion rules of an attraction-repulsion system. The simulation used to train the GNN consists of 4800…

create_fig_4.py

Training GNN on boids (16 types)

Particles

GNN Training

This script generates figures shown in Supplementary Figures 4, 11 and 12. A GNN learns the motion rules of boids (https://en.wikipedia.org/wiki/Boids). The simulation used…

create_fig_boids.py

Training GNN on gravity-like system

Particles

GNN Training

This script generates Supplementary Figure 7. A GNN learns the motion rules governing a gravity-like system The simulation used to train the GNN consists of 960 particles of…

create_fig_gravity.py

Training GNN on reaction-diffusion (rock-paper-scissors)

Mesh

GNN Training

This script generates Supplementary Figure 17. It showcases a Graph Neural Network (GNN) learning the dynamics of a reaction-diffusion system. The training simulation…

create_fig_rps.py

Training GNN on signaling

Signaling

GNN Training

This script generates figures shown in Supplementary Figures 18. A GNN is trained on a signaling network (998 nodes, 17,865 edges). Note 100 of datasets are generated for…

create_fig_signal.py

Training GNN on wave propagation

Mesh

GNN Training

This script generates Supplementary Figure 15. It demonstrates how a Graph Neural Network (GNN) learns the rules of wave propagation. The training simulation consists of 1E4…

create_fig_wave.py

Wave propagation with different diffusion coefficients

Mesh

Simulation

This script creates the fifth column of paper’s Figure 2. Simulation of wave-propagation over a mesh of 1E4 nodes with variable propagation-coefficients.

create_fig_2_5.py