Training GNN on wave propagation

This script generates Supplementary Figure 15. It demonstrates how a Graph Neural Network (GNN) learns the rules of wave propagation. The training simulation consists of 1E4 mesh observed over 8E3 frames. Nodes interact via wave propagation with type-dependent coefficients.

First, we load the configuration file and set the device.

config_file = 'wave_slit'
figure_id = 'supp15'
config = ParticleGraphConfig.from_yaml(f'./config/{config_file}.yaml')
device = set_device("auto")

The following model is used to simulate the wave-propagation model with PyTorch Geometric.

class WaveModel(pyg.nn.MessagePassing):
    """Interaction Network as proposed in this paper:
    https://proceedings.neurips.cc/paper/2016/hash/3147da8ab4a0437c15ef51a5cc7f2dc4-Abstract.html"""

    """
    Compute the Laplacian of a scalar field.

    Inputs
    ----------
    data : a torch_geometric.data object
    note the Laplacian coeeficients are in data.edge_attr

    Returns
    -------
    laplacian : float
        the Laplacian
    """

    def __init__(self, aggr_type=[], beta=[], bc_dpos=[], coeff=[]):
        super(WaveModel, self).__init__(aggr='add')  # "mean" aggregation.

        self.beta = beta
        self.bc_dpos = bc_dpos
        self.coeff = coeff

    def forward(self, data):
        x, edge_index, edge_attr = data.x, data.edge_index, data.edge_attr

        c = self.coeff
        u = x[:, 6:7]

        laplacian_u = self.propagate(edge_index, u=u, edge_attr=edge_attr)
        dd_u = self.beta * c * laplacian_u

        self.laplacian_u = laplacian_u

        return dd_u

    def message(self, u_j, edge_attr):
        L = edge_attr[:,None] * u_j

        return L


def bc_pos(x):
    return torch.remainder(x, 1.0)


def bc_dpos(x):
    return torch.remainder(x - 0.5, 1.0) - 0.5

The coefficients of diffusion are loaded from a tif file specified in the config yaml file and the data is generated.

Vizualizations of the wave propagation can be found in “decomp-gnn/paper_experiments/graphs_data/graphs_wave_slit/”

If the simulation is too large, you can decrease n_particles and n_nodes in “wave_slit.yaml”.

model = WaveModel(aggr_type=config.graph_model.aggr_type, beta=config.simulation.beta)

generate_kwargs = dict(device=device, visualize=True, run_vizualized=0, style='color', erase=False, save=True, step=50)
train_kwargs = dict(device=device, erase=True)
test_kwargs = dict(device=device, visualize=True, style='color', verbose=False, best_model='20', run=0, step=20)

data_generate_mesh(config, model , **generate_kwargs)

Initial configuration of the simulation. There are 1E4 nodes. The colors indicate the node scalar values.

Frame 7500 out of 8000

The GNN model (see src/ParticleGraph/models/Mesh_Laplacian.py) is optimized using the simulated data.

Since we ship the trained model with the repository, this step can be skipped if desired.

if not os.path.exists(f'log/try_{config_file}'):
    data_train(config, config_file, **train_kwargs)

The model that has been trained in the previous step is used to generate the rollouts.

data_test(config, config_file, **test_kwargs)

Finally, we generate the figures that are shown in Supplementary Figure 15. The results of the GNN post-analysis are saved into ‘decomp-gnn/paper_experiments/log/try_wave_slit/results’.

config_list, epoch_list = get_figures(figure_id, device=device)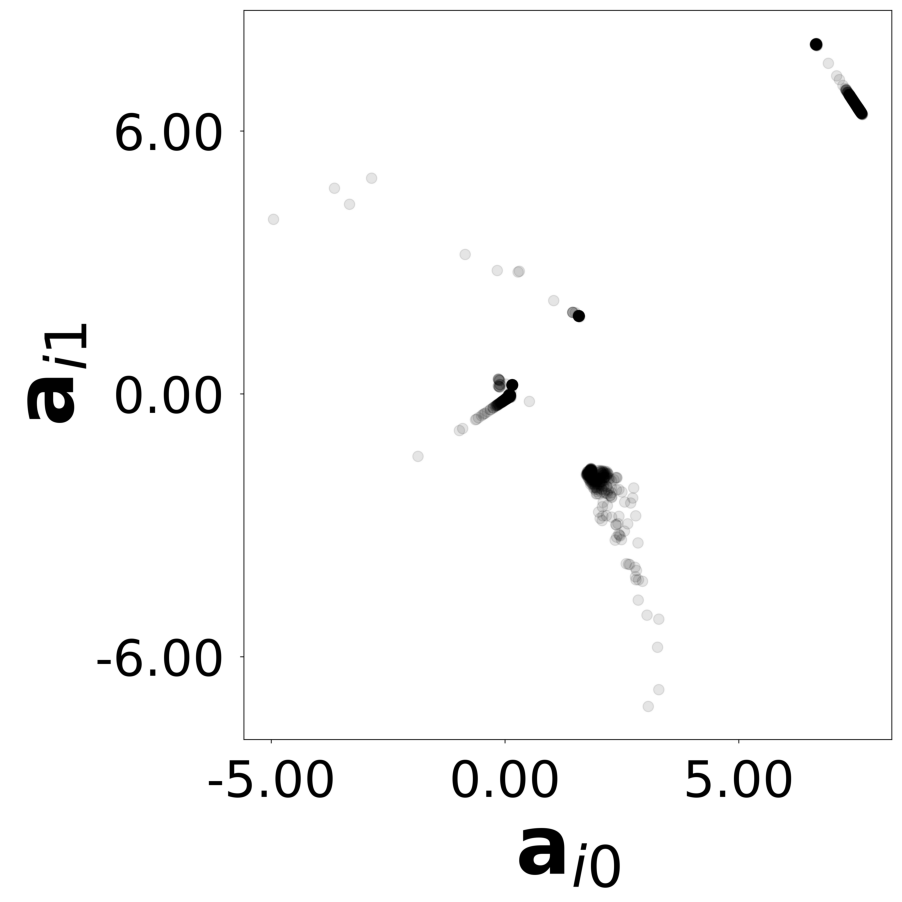

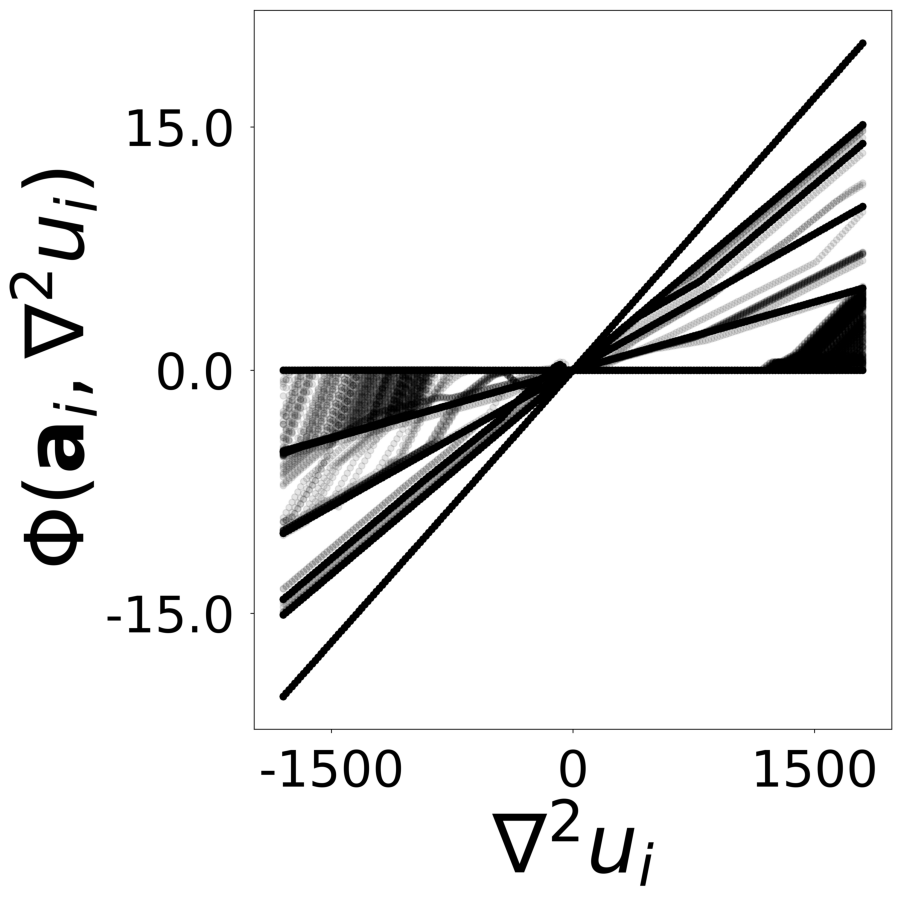
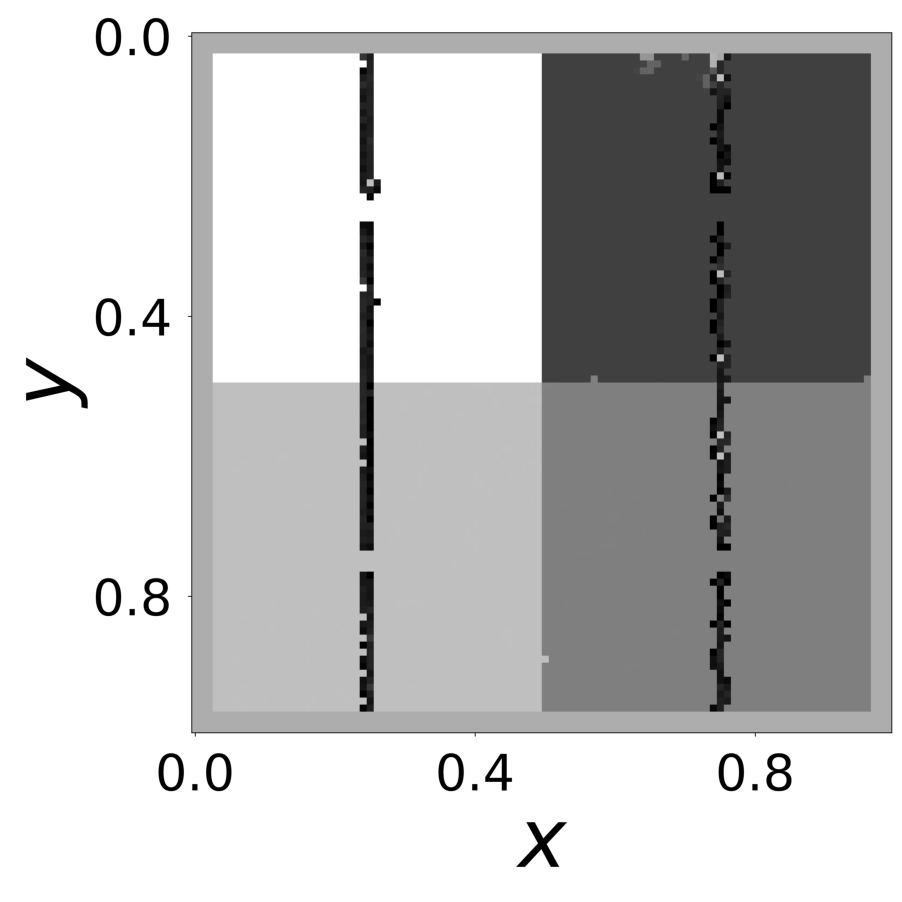
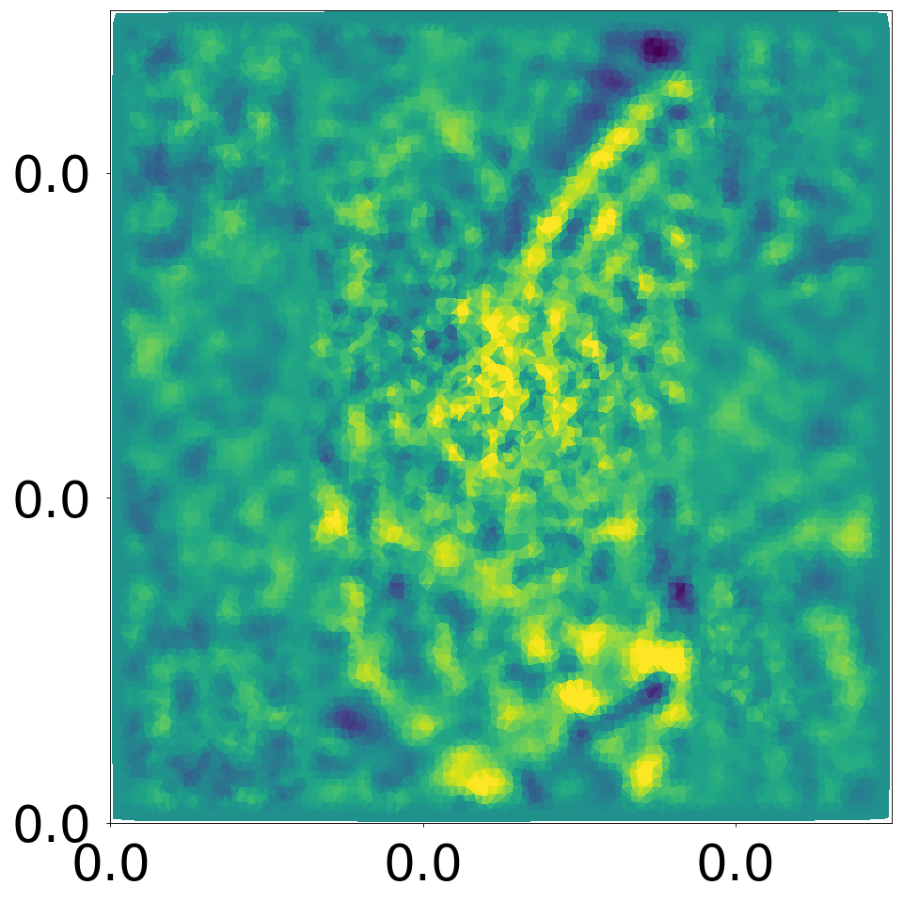
Learned latent vectors (x1E4)

Learned interaction functions (x1E4)

Learned map of the wave propagation coefficients

GNN rollout inference at frame 7980

All frames can be found in “decomp-gnn/paper_experiments/log/try_wave_slit/tmp_recons/”